Post Quantum encryption based on Lattices
In the last four decades, many widely used public key cryptographic schemes have been designed based on the difficulty of factoring and other similar problems. That includes RSA, the Diffie-Hellman Key Exchange and Elliptic curve crypto. However is a quantum computer gets built we can use Shor’s algorithm to solve factoring with exponential speedup and search with Grover’s algorithm with polynomial speedup which would mean that these encryption schemes can be easily broken.
It has been shown that lattice-based cryptography is one of the quantum resistant encryption schemes.
A lattice can basically be thought of as any regularly spaced grid of points stretching out to infinity.
Vector
A vector is nothing more than a fancy name for a point, a tuple of numbers called the coordinates of the vector. So (2,3) is a particular 2-dimensional vector as it has 2 coordinates, and a lattice is a collection of evenly spaced vectors. A special vector of interest is the origin which is the vector with all coordinates set to 0. For example, in 3 dimensions, the origin is (0, 0, 0). We say that a vector is long if it is far away from the origin. Conversely, a vector is short if it is close to the origin.
Basis
Lattices are infinitely large objects but computers only have a finite amount of memory to work with. So we will need a succinct way to represent lattices if we are going to use them in cryptography. For this, we use what is called a basis of a lattice. A basis is a small collection of vectors that can be used to reproduce any point in grid that forms the lattice.
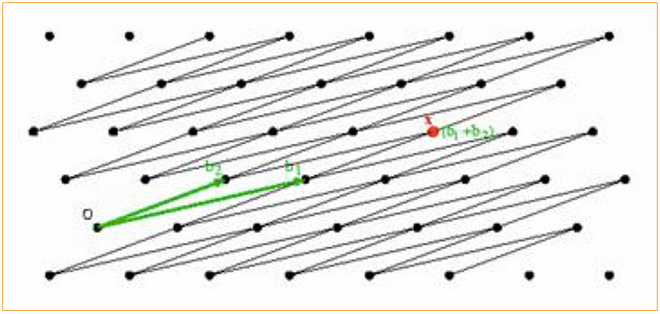
Let’s look at the case of a 2-dimensional lattice, a grid of points on a flat surface like a piece of paper. First, choose two more points that don’t happen to lie on a single line going through the origin. For example, we could choose (2,0) and (0,2). Here is how these points can be used to generate a third point:
First we choose two whole numbers; say, 3 and -1. We multiply the coordinates of the first point by 3 to get the point (6,0) and the coordinates of the second point by -1 to get (0,-2). Now we add the results together to get our new point (6,-2). Using this method, we can use (2,0) and (0,2) to generate an entire grid of evenly spaced points, namely all those with coordinates (x,y) such that both x and y are even numbers where we also count 0 as an even number. In other words, the basis consisting of vectors (2,0) and (0,2) generates the lattice points with even coordinates. The idea is that by choosing a basis we have actually chosen an entire lattice, namely the one whose points are generated by the vectors in the basis. Crucially, in contrast to an infinite grid of points, a basis is a simple finite object which we can represent in a computer’s memory.
An important thing to notice is that any given lattice doesn’t have just one basis. In fact, it has many basis. For example, instead of using (2,0) and (0,2) above we could have just as well chosen (-2,0) and (0, -2) or even (4, 2) and (2, 2). In each case they end up generating the exact same grid of points.
We say that a basis is short if it consist of short vectors (See the blue basis in the Figure below). Conversely, we say that a basis is long if it consists only of long vectors (See the green basis in the Figure 2 below). It turns out that short basis are much more useful than long ones when it comes to solving the types of hard lattice problems cryptographers are interested in.
Closest vector problem (CVP)
In CVP, a basis of a vector space V and a metric M (often $L^2$) are given for a lattice L, as well as a vector v in V but not necessarily in L. It is desired to find the vector in L closest to v (as measured by M).
At first glance, this might seem like a relatively easy problem to solve. However, notice that the basis we are given consist of long vectors. So it’s not immediately clear how they can be combined to generate a point with only small coordinates, namely a short vector. Moreover, when it comes to cryptography, we’re really talking about lattices in much higher dimensions (e.g. 10,000 instead of just 2 as in our examples above). That means that our points actually have 10,000 coordinates, not 2 coordinates. So finding a combination of the basis vectors that simultaneously makes all 10,000 generated coordinates small turns out to be quite hard, so much so that we don’t know how to solve the problem quickly even with a quantum computer, let alone a conventional one.
The Goldreich–Goldwasser–Halevi (GGH) Cryptosystem
GGH is an asymmetric cryptosystem based on lattices that can be used for encryption. Lattices are pretty cool because lattice-based cryptography has some very interesting properties (some lattice-based cryptosystems are believed to be quantum resistant!).
GGH takes advantage CVP’s assumed difficulty for “bad” bases to create an asymmetric key pair. A GGH keypair consists of two bases for the same lattice: one public, one private. A plaintext message is encoded as a vector with integer coefficients and a ciphertext is a vector that is not a lattice point.
In a GGH keypair, a public key is a “bad” basis and a private key is a “good” basis. A “good” basis is a relatively orthogonal with short basis vectors. There are algorithms for approximating CVP for a “good” basis. One such algorithm is called Babai’s Closest Vector algorithm.
Encryption
Given a message $m = \left( m _ { 1 } , \ldots , m _ { n } \right)$ error $e$ and public key $B ^ { \prime }$ compute
Decryption
To decrypt the cyphertext one computes
The Babai rounding technique will be used to remove the term $\ e \cdot B ^ { - 1 }$ as long as it is small enough. Finally compute
import math
import random
import numpy as np
from random import randint
import base64
import binascii
from scipy import linalg
#from libLLL import *
"""
Here we generate a public and private key using an orthogonal private key
and a nearly parallel public key
n is the security parameter given
"""
def keyGeneration(n):
privateB=[]
print("Searching for private vectors")
ratio = 1
"""
while True:
#iterations = iterations + 1
privateB=np.random.random_integers(-10,10,size=(n,n))
#privateB=gram_schmidt_columns(privateB)
privateB=np.array( lll_reduction(privateB))
ratio =hamdamard_ratio(privateB,n)
print(ratio)
if(ratio >= .8 and ratio <= 1):
privateB=privateB.astype(int)
break
"""
privateB=np.identity(n)
#privateB =linalg.orth(np.random.random_integers(-10,10,size=(n,n))).astype(int)
print(privateB)
print("Looking for public vector")
while True:
badVector = rand_unimod(n)
temp=np.matmul(privateB,badVector)
ratio = hamdamard_ratio(temp,n)
if ratio <= .1:
publicB=temp
break
print(publicB)
return privateB,publicB,badVector
def gram_schmidt_columns(X):
Q, R = np.linalg.qr(X)
return Q
"""
This function is used to determine how orthogonal the matrix is
close to 1 = orthogonal
close to 0 = parallel vectors
"""
def hamdamard_ratio(basis,dimension):
detOfLattice = np.linalg.det(basis)
mult=1
for v in basis:
mult = mult * np.linalg.norm(v)#(np.sqrt((v.dot(v))))
hratio = (detOfLattice / mult) ** (1.0/dimension)
return hratio
"""
This method is used to encrypt a text file with the public vector
Multiplication should be performed as
v_1 * b_1 + v_2 * b_2 ... V_n * B_n
"""
def encrypt(fileName, publicB):#needs extension to new keys <---
#publicB = [[1,45],[1,-45]] # making my own public basis b
encoded = []
with open(fileName,'r') as f:
for line in f:
for c in line:
encoded.append(base64.b64encode(bytes( c,"utf-8") ) )
print("\n--------ENCODED TEXT--------\n",encoded)
binaryMessage=[]
for i in range(len(encoded)):
binaryMessage.append( binascii.a2b_base64(encoded[i]) )
#print(binaryMessage)
encrypted_ints = []
for i in range(len(encoded)):
encrypted_ints.append( int.from_bytes(binaryMessage[i],byteorder='little') )
cyphertext =[]
for i in range(len(encoded)):
#cyphertext.append(np.multiply( int.from_bytes(encrypted[i],byteorder='little') ,publicB[i]))
cyphertext = np.matmul( encrypted_ints, publicB)
random_vector = np.random.randint(-10,10,size=(1,len(publicB)))
#cyphertext = cyphertext + random_vector
print("--------CYPHER ARRAY--------\n",cyphertext)
return cyphertext
"""
This will take a cyphertext and revert it back to its original form
"""
def decrpyt(cipherText,privateBasis,publicB,unimodular):
A = privateBasis
x = cipherText
BPRIME = np.linalg.inv(A)
BB = np.matmul(BPRIME,x)
unimodular1 = np.linalg.inv(unimodular)
m =np.round(np.matmul(BB,unimodular1)).astype(int)#np.round(np.matmul(BB,unimodular1)).astype(int)
print("\n--------MESSAGE ARRAY--------\n",m)
return m
"""
This function will create a random unimodular matrix that will be used to transform our public vector
"""
def rand_unimod(n):
random_matrix = [ [np.random.randint(-10,10,) for _ in range(n) ] for _ in range(n) ]
upperTri = np.triu(random_matrix,0)
lowerTri = [[np.random.randint(-10,10) if x<y else 0 for x in range(n)] for y in range(n)]
#we want to create an upper and lower triangular matrix with +/- 1 in the diag
for r in range(len(upperTri)):
for c in range(len(upperTri)):
if(r==c):
if bool(random.getrandbits(1)):
upperTri[r][c]=1
lowerTri[r][c]=1
else:
upperTri[r][c]=-1
lowerTri[r][c]=-1
uniModular = np.matmul(upperTri,lowerTri);
return uniModular
"""debugging methods"""
def show_message(message):
print("--------MESSAGE--------")
for i in range(len(message)):
letter =chr(abs(message[i]))
print(letter,end="")
print()
def write_block(publicB):
file = open('ggh_block.txt','w')
file.write("------BEGIN GGH PUBLIC KEY BLOCK -----\n")
for row in range(len(publicB)):
for col in range(len(publicB)):
encoded = base64.b64encode(publicB[row][col] )
file.write(str(encoded)[8:13])
file.write("\n")
file.write("\n--------END GGH PUBLIC KEY BLOCK -------")
file.close()
def display_matrix(matrix):
for row in range(len(matrix)):
for col in range(len(matrix)):
print(matrix[row][col], " ", end="" )
print("\n")
def check_determinant(matrix):
det=1
for i in range(len(matrix)):
for j in range(len(matrix)):
if i ==j:
det = det * matrix[i][j]
return det
"""end debugging methods"""
if __name__ == "__main__":
#rand = rand_unimod(48)
while True:
try:
security_parameter = int(input("Please enter a security parameter: "))
file_name = str(input("Please enter a file name with extension: "))
break;
except ValueError:
print("Incorrect input")
alice = keyGeneration(security_parameter)
write_block(alice[1])
bob = encrypt(file_name,alice[1])
alice_recives = decrpyt(bob,alice[0],alice[1],alice[2])
show_message(alice_recives)
#pprint(np.asarray(alice_recives))