Deep Learning Basics
Deep learning is part of a broader family of machine learning methods based on learning data representations, as opposed to task-specific algorithms. Learning can be supervised, semi-supervised or unsupervised

Gradient Descent
Most deep learning algorithms involve optimization of some sort. Optimization refers to the task of either minimizing or maximizing some function f (x) by altering x. The function we want to minimize or maximize is called the objective function or the cost function . We can reduce f (x) by moving x in small steps with opposite sign of the derivative to get to the minima (Local or global depending on the function) .This technique is called gradient descent.
For functions with multiple inputs, we must make use of the concept of partial derivatives. The partial derivative $\frac { \partial } { \partial x _ { i } } f ( x )$ measures how f changes as only the variable $x _ { i }$ increases at point x . The gradient of f is the vector containing all of the partial derivatives, denoted by $\nabla _ { \boldsymbol { x } } f ( \boldsymbol { x } )$
The new point is proposed using the below equation where $\epsilon$ is the learning rate which determines the step size.
Mini-batch gradient descent
In large-scale applications the training data can have on order of millions of examples. It is computationally wasteful to compute the full loss function over the entire training set in order to perform only a single parameter update.Instead we compute the gradient over batches of the training data.A typical batch size contains 256 examples from the entire training set(Epoch) . This batch is then used to perform a parameter update.
Second order Optimization
We can also think of using the second derivative as it measures curvature to achieve faster convergence.
The Hessian matrix H(f)(x) is defined as:
A popular group of methods for optimization in context of deep learning is based on Newton’s method, which iterates the following update:
Multiplying by the inverse Hessian leads the optimization to take more aggressive steps in directions of shallow curvature and shorter steps in directions of steep curvature. Note, crucially, the absence of any learning rate hyperparameters in the update formula, which the proponents of these methods cite this as a large advantage over first-order methods.
However, the update above is impractical for most deep learning applications because computing (and inverting) the Hessian in its explicit form is a very costly process in both space and time. For instance, a Neural Network with one million parameters would have a Hessian matrix of size [1,000,000 x 1,000,000] which is computationally expensive. There are algorithms such as L-BFGS, which uses the information in the gradients over time to form the approximation implicitly (i.e. the full matrix is never computed). However these do not work in mini batch settings hence are not commonly used with Deep learning.
Instead of initializing the weights in a purely random manner, Xavier initialization enables to have initial weights that take into account characteristics that are unique to the architecture. If W is the weights gaussian distribution and N is the number of neurons.
To reduce dependence on initialization we use Batch Norm . It is usually done after a fully connected/convolutional layer and before a non-linearity layer and aims at allowing higher learning rates. $\gamma ,\beta$ are the hyperparameters while $\mu , \sigma$ are the mean and variance of the batch which we want to normalize.
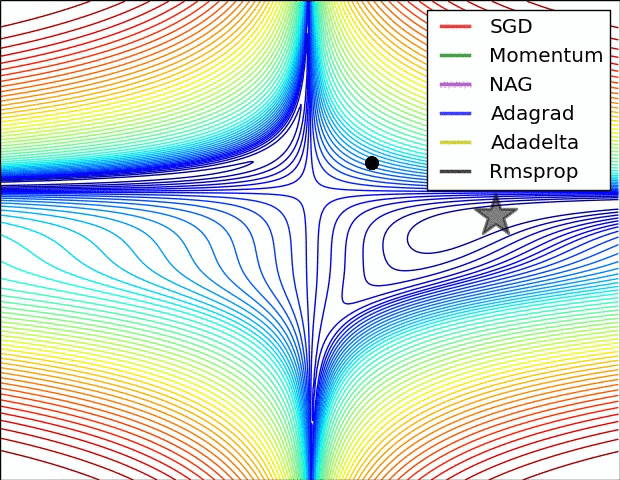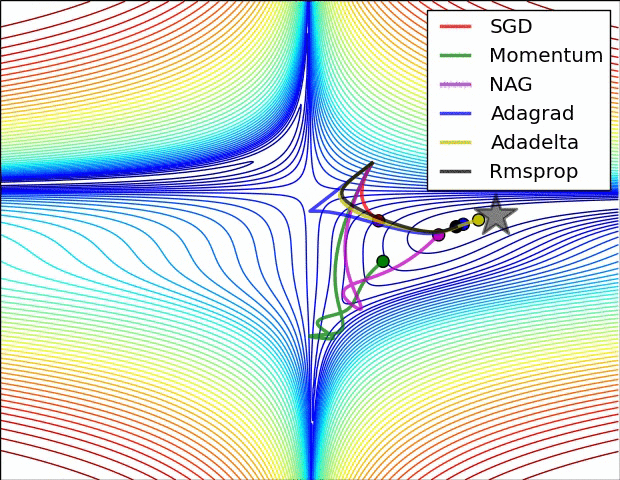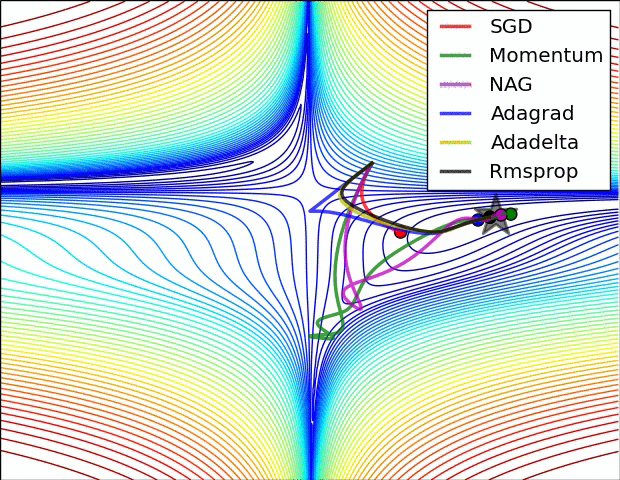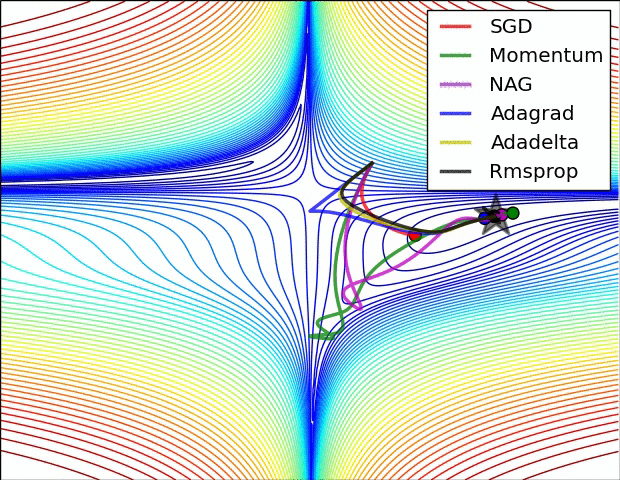
There are other optimization methods with adaptive learning rates

Feedforward neural networks
In this network, the information moves in only one direction, forward, from the input nodes, through the hidden nodes (if any) and to the output nodes. There are no cycles or loops in the network.

| With an appropriate loss function on the neuron’s output, we can turn a single neuron into a linear classifier such as binary Softmax classifier. We can interpret $\sigma \left( \sum _ { i } w _ { i } x _ { i } + b \right)$ to be the probability of one of the classes $P \left( y _ { i } = 1 | x _ { i } ; w \right)$ adn the probability of the other class would be $P \left( y _ { i } = 0 | x _ { i } ; w \right) = 1 - P \left( y _ { i } = 1 | x _ { i } ; w \right)$ |
Some of the commonly used activation functions are Sigmoid $\sigma ( x ) = 1 / \left( 1 + e ^ { - x } \right)$ , Tanh $\tanh ( x ) = 2 \sigma ( 2 x ) - 1$ , RELU(Rectified linear unit) $f ( x ) = \max ( 0 , x )$ , Leaky Relu $f ( x ) = 1 ( x < 0 ) ( \alpha x ) + 1 ( x > = 0 ) ( x )$ where $\alpha$ is a small constant
The universal approximation theorem (Hornik et al., 1989; Cybenko, 1989) states that a feedforward network with a linear output layer and at least one hidden layer with any “squashing” activation function can approximate any function from one finite-dimensional space to another with any desired non-zero amount of error, provided that the network is given enough hidden units.

The universal approximation theorem means that regardless of what function we are trying to learn, we know that a large MLP will be able to represent this function. However, we are not guaranteed that the training algorithm will be able to learn that function.
Back-Propagation
When we use a feedforward neural network to accept an input x and produce an output ˆ y, information flows forward through the network. The inputs x provide the initial information that then propagates up to the hidden units at each layer and finally produces yˆ. This is called forward propagation. During training, forward propagation can continue onward until it produces a scalar cost J (θ). The back-propagation algorithm (Rumelhart et al., 1986a), often simply called backprop, allows the information from the cost to then flow backwards through the network, in order to compute the gradient.
The derivative with respect to weight W is computed using chain rule and is of the following form:
The weights are updated as follows:
Updating weights ― In a neural network, weights are updated as follows:
- Step 1: Take a batch of training data.
- Step 2: Perform forward propagation to obtain the corresponding loss.
- Step 3: Backpropagate the loss to get the gradients.
- Step 4: Use the gradients to update the weights of the network.
Let us see an example of a Sigmoid with a 2-dimensional neuron (with inputs x and weights w) for Back prop
We can group multiple gates into a single gate, or decompose a function into multiple gates whenever it is convenient for computation.

This decomposition of the network to graphs is done automatically in modern deep learning packages. The gradients are calculated automatically using reverse mode auto differentiation. The core ideas behind modern feedforward networks have not changed substantially since the 1980s. The same back-propagation algorithm and the same approaches to gradient descent are still in use. Most of the improvement in neural network performance from 1986 to now can be attributed to larger datasets and to more powerful computers.
Regularization
We can use the L1(Lasso) and L2(Ridge) regularization from statistical machine learning.
L1 regularization is defined as $\lambda | \theta | _ { 1 }$ while L2 regularization is defined as $\lambda | \theta | _ { 2 } ^ { 2 }$
Dropout is a regularization technique for reducing overfitting in neural networks by preventing complex co-adaptations on training data. It drops out neurons with probability p > 0 and forces the model to avoid relying too much on particular sets of features.

Convolutional Networks
Convolutional neural networks or CNNs, are a specialized kind of neural network for processing data that has a known, grid-like topology. Examples include time-series data, which can be thought of as a 1D grid taking samples at regular time intervals, and image data, which can be thought of as a 2D grid of pixels. They are simply neural networks that use convolution in place of general matrix multiplication in at least one of their layers.
Convolution layer (CONV)
The convolution layer (CONV) uses filters that perform convolution operations as it is scanning the input I with respect to its dimensions. Its hyperparameters include the filter size F(Dimension F x F X C) and stride S. The resulting output O is called feature map or activation map(Dimension O x O X 1). We can also Pad the image with Zeros to match the size of image to dimensions of the filter and stride.

Convolution leverages three important ideas that can help improve a machine learning system: sparse interactions, parameter sharing and equivariant representations. Sparse interactions is accomplished by making the kernel smaller than the input , Parameters are shared across the image space and due to the convolution operation we have equivariance to translation which means that if the input changes, the output changes in the same way.
Pooling layer (POOL)
The pooling layer (POOL) is a downsampling operation, typically applied after a convolution layer, which does some spatial invariance. In particular, max and average pooling are special kinds of pooling where the maximum and average value is taken.

Fully Connected (FC) layer
The fully connected layer (FC) operates on a flattened input where each input is connected to all neurons.

Recurrent Neural Networks
Recurrent neural networks or RNNs (Rumelhart et al., 1986a) are a family of neural networks for processing sequential data. RNNs can scale to much longer sequences as well as process sequences of variable length. Parameter sharing makes it possible to extend and apply the model to examples of different forms (different lengths, here) and generalize across them. A related idea is the use of convolution across a 1-D temporal sequence. There are many types of RNN which are listed below

The most effective sequence models used in practical applications are called gated RNNs. These include the long short-term memory and networks based on the gated recurrent unit. Plain RNNs have the issue of vanishing gradient and exploding gradient which makes it difficult to capture long term dependencies. Hence gated RNNs with gradient clipping is used in practice.
Long Short-Term Memory units (LSTM)
Is a vanilla RNN the output per step is as follows.
To deal with the vanishing gradient problem instead of one output LSTM outputs 2 vectors at every step $C _ { t } , h _ { t }$ which is defined as follows
Where C is the cell state and H is the output of that step
$\odot$ indicates the Hadamard product(element-wise product).
I is the input gate , F is the forget gate and O is the output gate. We operate on the cell state C using the I,F,O,G gates and update the C value to Zero(to reset it) or some other value as required.

Gated Recurrent Unit (GRU)
GRU is similar to LSTM but has lesser gates but provide similar performance to LSTM .
Where x is the input ,h is the output , z is the update gate , r is the reset gate.